• Главная
• О журнале
  • О журнале
  • Распространение
  • Редакционный совет
  • Редакция
  • Рубрики
  • Список рецензентов статей
  • Правила рецензирования
  • Авторы
  • Russian Logistics Journal
• Новости
  • Календарь мероприятий
  • Размещение пресс-релизов
  • Новости логистики
• Подписка
  • Подписка через агентства
  • Редакционная подписка
  • Электронная рассылка
• Реклама
  • Реклама в журнале
  • Реклама на сайте
• Архив
• Контакты

Проблемы многокритериальной оптимизации запасов с учетом рисков

Для задач выбора наилучшего решения при управлении запасами по многим критериям, дана иллюстрация феноменов неадекватной оптимизации в формате традиционных методов. Подчеркивается необходимость разработки новых подходов к оптимизации, чтобы дать менеджеру возможность устранять такие феномены.

Скачать статью в формате PDF

ПРОБЛЕМЫ МНОГОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ ЗАПАСОВ С УЧЕТОМ РИСК

ГЕННАДИЙ БРОДЕЦКИЙ, ГУ-ВШЭ, профессор, д.т.н

Аннотация

Для задач выбора наилучшего решения при управлении запасами по многим критериям, дана иллюстрация феноменов неадекватной оптимизации в формате традиционных методов. Подчеркивается необходимость разработки новых подходов к оптимизации, чтобы дать менеджеру возможность устранять такие феномены.

Ключевые слова

управление запасами, многокритериальная оптимизация, учет рисков, феномен неадекватного выбора.

Annotation

For problems of a choice of the best decision at stock management by many criteria, the illustration of phenomena of inadequate optimization in a format of traditional methods is given. Necessity of working out of new approaches to optimization is underlined to give the chance to the manager to eliminate such phenomena.

Keywords

stock management, multicriterion optimization, the account of risks, a phenomenon of an inadequate choice.

Введение

При управлении запасами лицо, принимающее решения (ЛПР), может ориентироваться на целый ряд критериев: их называют частными критериями. Например, они могут быть обусловлены одновременными требованиями снижения издержек поставок и хранения товаров, требованиями минимизации средств, «замороженных» в запасах таких товаров. Кроме того, другие частные критерии могут быть обусловлены также требованиями снижения различных рисков для соответствующих цепей поставок. При этом задача управления запасами может быть сформулирована, как задача многокритериальной оптимизации. В [1] уже была дана иллюстрация возможностей решения задач такого типа на основе специального подхода к оптимизации, который был представлен в [2].

Оптимизация систем управления запасами по многим критериям — это исключительно новая, еще слабо изученная область логистики. В реальных ситуациях при решении задач такого типа менеджер может столкнуться с проявлениями нежелательных феноменов, которые затруднят обоснование выбора наилучшего решения. Их устранение может стать большой проблемой. Материалы этой статьи проиллюстрируют этот аспект проблемы и необходимость разработки новых критериев выбора для решения задач многокритериальной оптимизации такого типа, чтобы позволить менеджеру устранять указанные феномены. Соответствующий круг вопросов впервые обсуждается применительно к задачам управления запасами. Представленные здесь материалы будут, несомненно, интересны и полезны многим менеджерам в области логистики.

Атрибуты модели управления запасами

Чтобы проиллюстрировать проблемы, которые могут возникать в формате задач оптимизации решений при многих критериях применительно к системам управления запасами, далее используем модель, которая была представлена в [1]. В указанной работе показано, что задача управления запасами в условиях риска может быть представлена как многокритериальная задача оптимизации. В частности, рассматриваются следующие частные критерии (структура их показателей приведена в [1]), которые требуют минимизации.

• Частный критерий С₁ — издержки доставки и хранения товара.
• Частный критерий С₂ — средства, «замороженные» в запасах.
• Частный критерий С₃ — средние ожидаемые потери из-за задержек доставки.
• Частный критерий С₄ — ожидаемые потери из-за производственного брака.

Рассматривается ситуация, когда предполагается поставлять товар от двух поставщиков (I и II). Решение включает:
• выбор поставщика (или поставщиков);
• оптимизацию размера заказа у выбранного поставщика (для поставщиков I и II), причем выбранным транспортным средством;
• учет возможности диверсификации поставок.

Как и в [1] для компактности изложения в качестве стратегии диверсификации поставок от поставщиков I и II далее анализируется только стратегия (1:1), при которой годовой объем поставок поровну покрывается указанными поставщиками.

Рассматриваются следующие альтернативы:
1) поставка товара только от поставщика I (альтернатива S₁);
2) поставка только от поставщика II (альтернатива S₂);
3) поставка 50% товара от поставщика I и 50% от поставщика II (альтернатива S₃).

Издержки на доставку от каждого из поставщиков и для каждого транспортного средства известны и, для удобств сравнения результатов оптимизации, оставлены такими же, как и в работе [1]. При диверсификации предусматривается возможность догрузки, что учтено в показателях соответствующих частных критериев. Далее, как и в [1], принято, что учитываемые риски обусловлены только следующими факторами: случайными задержками поставок; случайной просрочкой платежа; случайными потерями из-за брака.

Это позволяет далее воспользоваться тем, что в указанной выше работе [1] уже были формализованы:
1) само дерево решений с учетом рисков;
2) структура оценок частных критериев, на основе которых реализуется оптимизация.

Указанное дерево решений здесь не приведено (из-за ограничений на объем статьи). Для иллюстрации проблем, которые могут возникнуть у менеджера при обосновании наилучшего решения, нам достаточно воспользоваться следующим. Результаты анализа в формате метода дерева решений позволили в [1] представить рассматриваемую задачу, как задачу выбора наилучшей альтернативы (из множества S₁, S₂, S3) при четырех частных критериях (это представленные выше критерии — С₁, С₂, С₃, С₄). Оценки альтернатив по этим частным критериям приведены в табл. 1.

Таблица 1

Показатели альтернатив по частным критериям

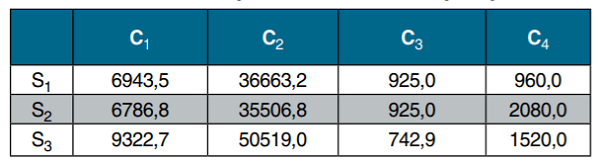
На последнем шаге алгоритма оптимизации по методу дерева решений, который представлен в [1] с использованием процедур свертки и блокировки [2], среди указанных альтернатив требуется выбрать наилучшее решение при заданных частных критериях. Может показаться, что это — обычная/ стандартная задача многокритериальной оптимизации. Оказывается, что нет. Проиллюстрируем, с какими проблемами столкнется менеджер, когда будет решать такую задачу при использовании различных традиционных методов многокритериальной оптимизации.

Выбор по методу минимаксного критерия

Процедуры такого подхода к минимизации частных критериев представлены в табл. 2. Решение определяется по минимальному элементу дополнительного столбца (в котором представлены наихудшие показатели по строкам).

Таблица 2

Выбор наилучшего решения по минимаксному критерию

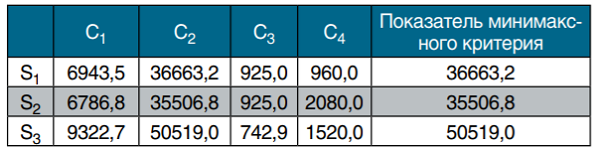
Наименьший показатель критерия в табл. 2 (он равен 35506,8) соответствует альтернативе S₂: надо выбрать второго поставщика. Однако, при обосновании выбора у менеджера возникнут трудности. Структура показателей табл. 2 такова, что она обусловила следующее. Феномен неадекватного выбора проявился явным образом: дополнительный столбец со значениями функции выбора сформирован только из показателей одного частного критерия С₂. Остальные частные критерии не оказывают влияния на выбор. Их присутствие здесь оказалось формальным. Вряд ли менеджер и ЛПР примут такое обоснование оптимального решения.

Выбор по методу взвешенных оценок частных критериев

Пусть, как и в [1], принято, что ЛПР задает следующие «веса» для оценок частных критериев. Для частного критерия С₁ вес составляет С₁=0,3; для С2 такой вес составляет С₂=0,4; для частного критерия С₃ он составляет С₃=0,1; а для частного критерия С₄ он составляет С₄= 0,2 (для наглядности эти веса представлены в последней строке табл. 3). Процедуры такого подхода к выбору решения приведены в табл. 3.

Таблица 3

Выбор по методу взвешенной суммы оценок частных критериев 

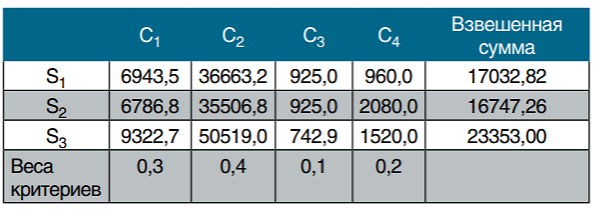
В последнем столбце табл. 3 выписаны результаты для взвешенных показателей каждой строки. Наименьший из них (он равен 16747,26) соответствует альтернативе S2. По этому методу надо выбрать второго поставщика. Однако, менеджера ждут трудности с обоснованием решения. Структура оценок в табл. 3 такова, что феномен доминирования снова проявляется. Легко видеть, что показатели третьего частного критерия (С3) практически не влияют на окончательный выбор (если формат процедур анализа не будет содержать третьего частного критерия, то выбор не изменится — проверьте это самостоятельно). Это же можно сказать и относительно показателей частного критерия С4. Выбор по методу обобщенного скалярного критерия Процедуры такого подхода к минимизации частных критериев представлены в табл. 4. Его формат предусматривает, что «веса» частных критериев не задаются ЛПР. Они определяются так, чтобы ориентировать выбор на утопическую точку (УТ) соответствующего поля издержек/потерь, т.е. точку с наилучшими/наименьшими значениями частных критериев. Модифицированные оценки частных критериев с учетом таких весов и значения функции выбора приведены в табл. 4.

Таблица 4

Выбор наилучшего решения по обобщенному скалярному критерию

Наименьшее значение функции выбора в табл. 4 (равно 4,301) соответствует альтернативе S₁. По этому методу надо выбрать первого поставщика. Однако, структура оценок в табл. 4 такова, что феномен доминирования снова проявляется: на выбор не влияют показатели частного критерия С3(если из процедур анализа, а также из табл. 4 удалить указанный частный критерий, то выбор не изменится — проверьте это самостоятельно).

Выбор по методу идеальной точки

Для реализации метода указывается утопическая точка (УТ). Точка в пространстве значений частных критериев, которая соответствует одной из анализируемых альтернатив и расположена на наименьшем расстоянии от УТ, дает наилучшее решение по методу идеальной точки. В формате рассматриваемой модели координатами утопической точки являются наилучшие показатели в столбцах табл. 5: УТ = (6786,8; 35506,8; 742,9; 960). «Расстояние» от альтернативы до утопической точки вычисляется по обычным формулам линейной алгебры. Это — корень квадратный из суммы квадратов разностей координат для УТ и анализируемой альтернативы. Такие «расстояния» представлены в табл. 5.

Таблица 5

Выбор наилучшего решения по методу идеальной точки

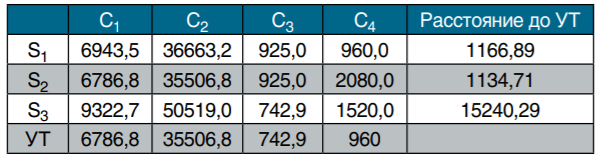
Наименьшее значение показателя критерия выбора, т.е. показателя расстояния до УТ (оно равно 1134,71 в табл. 5), соответствует альтернативе S₂. Наилучший выбор по методу идеальной точки — это выбор второго поставщика. Формат этого критерия также обнаруживает явные признаки феномена доминирования. Оптимальный выбор определился, как легко видеть, только по первому и по второму частным критериям (в связи с преобладанием их показателей в абсолютном выражении над показателями остальных критериев). Если частные критерии С₃ и С₄ удалить из анализа, то при оптимизации решения в таком формате задачи оптимизации выбор по методу идеальной точки останется таким же — проверьте это самостоятельно.

Выбор по методу критерия среднего геометрического

Наилучшее решение определяется по наименьшему из показателей среднего геометрического всех оценок частных критериев (по строкам таблицы). Выбор не изменится, если использовать показатель произведения всех оценок частных критериев: такой подход к оптимизации называют критерием произведений. Требуемые процедуры представлены в табл. 6 (в формате критерия произведений).

Таблица 6.

Выбор наилучшего решения по критерию среднего геометрического

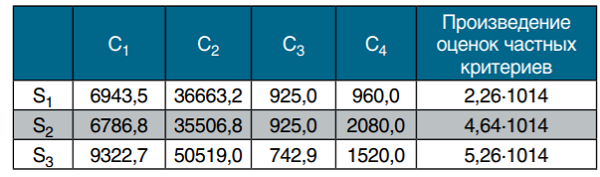
Наименьшее значение показателя дополнительного столбца (оно равно 2,26∙1014) соответствует альтернативе S₁. По этому методу выбирается поставщик I. Чтобы установить имеются или нет признаки доминирования одних частных критериев над другими, надо перейти к другому представлению показателей частных критериев. Вместо исходно заданных показателей частных критериев надо рассмотреть их логарифмы (по любому основанию большему, чем единица). Тогда показатели функции выбора будут представлены суммой указанных логарифмов оценок частных критериев. При этом ранжирование альтернатив не изменится, но структура показателей будет более прозрачной и позволит установить, имеются ли признаки доминирования и неадекватного выбора. Указанные процедуры представлены в табл. 7, причем использован переход к десятичным логарифмам оценок частных критериев. Вместо произведений элементов таблицы по строкам (как это было сделано в табл. 6) находится сумма полученных логарифмов оценок.

Таблица 7

Выбор наилучшего решения по методу среднего геометрического (переход к логарифмам показателей частных критериев)

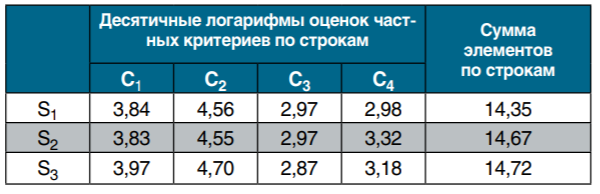
Как видим, и в формате этого критерия структура указанных слагаемых иллюстрирует частичное воздействие феномена неадекватного выбора: показатели первого и третьего частных критериев, практически, не влияют на выбор наилучшего решения (если эти частные критерии априори удалить из анализа, то при оптимизации решения по критерию среднего геометрического выбор останется таким же — проверьте это самостоятельно). Учитывая важность этих показателей, вряд ли и менеджер, и ЛПР примут такое обоснование оптимального решения.

Заключение

В этой статье применительно к задачам нахождения наилучших решений по многим критериям при управлении запасами дана иллюстрация возможного воздействия феномена неадекватного выбора. Указанные феномены для задач рассматриваемого типа, как было проиллюстрировано, действительно имеют место в формате традиционных критериев выбора, которые могли бы быть использованы при оптимизации решения. Таким образом, в статье проиллюстрировано, что располагаемый менеджером арсенал традиционных критериев выбора, которые можно использовать без опаски воздействия указанного нежелательного феномена в формате задач управления запасами при многих критериях, будет значительно урезан. Это может сделать проблемной саму возможность обеспечения адекватного выбора наилучшей альтернативы/ решения в практических ситуациях применительно к задачам рассмотренного типа. Указанная особенность подчеркивает необходимость разработки специальных новых процедур выбора, свободных от воздействия указанных выше феноменов, чтобы можно было включить их в арсенал инструментов менеджера при решении таких задач.

Библиографический список:

1. Бродецкий Г.Л., Гусев Д.А., Левина Т.В. Возможности многокритериальной оптимизации запасов с учетом рисков в формате метода дерева решений. Журн. «Логистика сегодня», № 6, 2008 г., с. 354—374.

2. Бродецкий Г.Л. Метод дерева решений при многокритериальной оптимизации в цепях поставок / «Логистика сегодня», № 5, 2008 г., с. 320—329.