• Главная
• О журнале
  • О журнале
  • Распространение
  • Редакционный совет
  • Редакция
  • Рубрики
  • Список рецензентов статей
  • Правила рецензирования
  • Авторы
  • Russian Logistics Journal
• Новости
  • Календарь мероприятий
  • Размещение пресс-релизов
  • Новости логистики
• Подписка
  • Подписка через агентства
  • Редакционная подписка
  • Электронная рассылка
• Реклама
  • Реклама в журнале
  • Реклама на сайте
• Архив
• Контакты

Возможности перераспределения рисков в цепях поставок в формате концепций чистых и коммерческих рисков

Рассматривается подход к эффективному перераспределению риска в цепях поставок на основе различных концепций риска. Решена задача определения доли участия в предложении рынка при заданной величине предельно допустимого риска в концепции коммерческих рисков и концепции чистых рисков.

Скачать статью в формате PDF

ВОЗМОЖНОСТИ ПЕРЕРАСПРЕДЕЛЕНИЯ РИСКОВ В ЦЕПЯХ ПОСТАВОК В ФОРМАТЕ КОНЦЕПЦИЙ ЧИСТЫХ И КОММЕРЧЕСКИХ РИСКОВ

ДЕНИС ГУСЕВ,
ГУ-ВШЭ, доцент, к.э.н.

Аннотация

Рассматривается подход к эффективному перераспределению риска в цепях поставок на основе различных концепций риска. Решена задача определения доли участия в предложении рынка при заданной величине предельно допустимого риска в концепции коммерческих рисков и концепции чистых рисков.

Ключевые слова

перераспределение риска, устойчивость цепей поставок, концепция чистых рисков, концепция коммерческих рисков, возможности доли участия в предложении бизнеса.

Annotation

The approach to the efficient redistribution of risk in supply chains based on different concepts of risk is considered in this article. The problem of determining volume of stake in the proposal of the market at a given maximum allowable risk in the concept of commercial risks and the concept of pure risk is solved.

Keywords

redistribution of risk, stability of supply chains, the concept of pure risk, the concept of commercial risk, the possibility of a stake in the business proposal.

Введение

Развитию методов управления рисками в цепях поставок уделяется большое внимание. Для обеспечения устойчивости цепей поставок в условиях риска и неопределенности разработана концепция комплексной безопасности цепей поставок [2]. Указанная концепция предусматривает пять иерархических уровней управления безопасностью цепей поставок (по убыванию важности): уровень регламентов, уровень методов управления риском, уровень управления событиями и процессами, уровень информационных технологий, уровень обеспечения физической безопасности груза. На каждом из этих уровней для менеджера прописываются общие правила управления безопасностью цепей поставок.

Как отмечается в [3], наиболее сложными являются три основные проблемы: выработка представлений о риске логистических операций, выявление пределов допустимого риска, разработка предложений по управлению риском в конкретной ситуации. Действительно, определенное представление менеджера о риске может предопределить и дальнейшие действия по управлению им. Как отмечено в [1], наиболее распространенными являются концепция чистых рисков и концепция коммерческих рисков. В концепции чистых рисков принимается, что отклонения от ожидаемого экономического результата возможны только в неблагоприятную сторону. При этом фактически оценивается только возможный «ущерб» при случайном неблагоприятном событии, и мерой риска является математическое ожидание потерь. В концепции коммерческих рисков анализируемый показатель может отклониться не только в неблагоприятную, но и в благоприятную сторону. При этом мерой риска будет уже среднеквадратическое отклонение (σ) экономического результата. Подчеркнем, что выбор лицом, принимающим решения (далее — ЛПР), одной из указанных двух концепций риска предопределяет и возможности выявления пределов допустимого риска и реализации мероприятий, направленных на управление риском.

Одним из наиболее доступных и эффективных действий является перераспределение риска. Такое перераспределение риска можно реализовать различными способами. Оно может осуществляться за счет, специально оговоренного лишь частичного, участия в реализации предложения рынка. А также, — за счет привлечения партнеров. Далее в статье рассмотрен подход к управлению рисками в цепях поставок на основе, именно, частичного участия ЛПР в предложении рынка в формате концепций коммерческих и чистых рисков. Подчеркнем, что наилучший выбор для разных ЛПР может быть различным. Это зависит от отношения ЛПР к риску и от формата поставленной задачи оптимизации при перераспределении риска.

Атрибуты моделируемой ситуации

Рассматривается условная ситуация [6], когда субъект рынка ЛПР(1) имеет возможность получить заказ на производство и поставку 20 000 единиц продукции. За каждую единицу продукции ЛПР(1) рассчитывает получить 2 у.е. прибыли. В случае срыва производства заказа в требуемом объеме на ЛПР будет наложен штраф в размере 3 у.е. за каждую единицу недопоставленной продукции.

При принятии решений ЛПР(1) руководствуется статистикой прошлых лет, показывающей, что для возможных реальных объемов выпуска такой продукции существуют следующие сценарии (в связи с возможными логистическими рисками срыва производства). Распределение вероятностей возможного выпуска продукции представлено в табл. 1.

Таблица 1

Сценарии выпуска у ЛПР(1)

Требуется определить долю участия в таком предложении, если известны допустимые пределы риска в формате концепций коммерческих и чистых рисков.

В формате концепции коммерческих рисков мерой риска является среднеквадратическое отклонение экономического результата. Пусть известно, что величину такого риска для данного ЛПР(1) необходимо ограничить величиной 16 000 у.е. Распределение вероятностей для объема выпуска продукции и соответствующих прибылей и возможных убытков при доле 100% участия в предложении представлено в табл. 2.

Таблица 2

Распределение вероятностей прибыли у ЛПР(1) при доле 100% участия в предложении

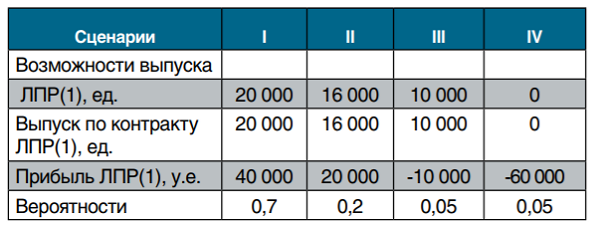
Соответствующие параметры анализируемого предложения при 100% участии (среднеквадратическое отклонение — σ; математическое ожидание — m) составят: σ = 23932,2, m = 28500. Таким образом, величина риска составляет 23932,2 у.е.

Такая величина риска неприемлема для ЛПР(1). Требуется снизить ее до 16 000 у.е. В такой ситуации можно легко оценить приближенно соответствующую долю α участия ЛПР(1) в рассматриваемом предложении, при которой будет выполнено ограничение, накладываемое на риск. Для этого можно составить соответствующее неравенство относительно неизвестного параметра α (полагая, что 0 ≤ α ≤ 1): 23932,2 • α ≤ 16 000. Отсюда найдем α ≤ 0,67. Это означает, что приемлемая доля участия ЛПР(1) в этом предложении составляет порядка 67%, чтобы риск составил не более требуемой величины 16 000 у.е.

Удостоверимся, что участие в данном предложении с долей 67% снижает риск до указанной величины. Соответствующее распределение вероятностей для прибыли при таком участии в предложении бизнеса представлено в табл. 3.

Таблица 3

Распределение вероятностей прибыли у ЛПР(1) при доле 67% участия в предложении

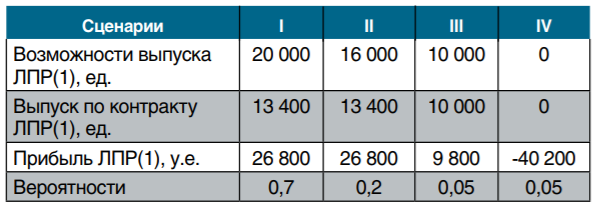
Соответствующие параметры анализируемого предложения при доле 67% участия (среднеквадратическое отклонение (σ); математическое ожидание (m)) составят: σ = 14874,8, m = 22600.

Таким образом, при указанной доле участия в предложении, показатель риска не превысит заданной величины. Более того, эти расчеты показывают, что найденная оценка для доли участия (67%) оказалась заниженной (то есть, допустима и большая доля участия в этом бизнесе без нарушения требований ограничения рисков). Это обусловлено тем, что выпуск продукции по контракту при долевом участии, вообще говоря, не будет пропорционален исходным возможностям выпуска продукции (см. табл. 3).

Формат концепции чистых рисков

Далее определим долю участия в предложении бизнеса в формате концепции чистых рисков. Пусть величина ожидаемых потерь, то есть чистых рисков для данного ЛПР (1) не должна быть большей 3 500 у.е. Поскольку в формате такой задачи управления риском нас интересуют именно потери, представим соответствующее распределение вероятностей для случайной величины потерь в случае участия в таком предложении на все 100%. Эти данные приведены в табл. 4.

Рассчитаем соответствующие средние ожидаемые потери (как показатель риска в формате концепции чистых рисков). Обозначим далее указанные средние ожидаемые потери, как П. Тогда имеем: П = 0*0,07+ 12 000*0,2+30000*0,05+60000*0,05 = 6 900 у.е. В этой ситуации также (как и в формате концепции коммерческих рисков) можно приближенно оценить соответствующую долю α участия ЛПР (1) в рассматриваемом предложении.

Таблица 4

Распределение вероятностей потерь для ЛПР(1) при доле 100% участия в предложении

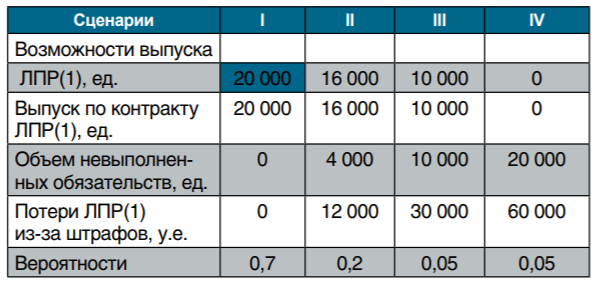
Для этого составим соответствующее неравенство относительно неизвестного параметра α. В формате концепции чистых рисков такое неравенство имеет вид (при 0 ≤ α ≤1): П • α ≤ 3 500. Учитывая, что П = 6 900, имеем: 6 900 • α ≤ 3 500. Отсюда найдем α ≤ 0,507. Итак, для ЛПР(1) доля участия в данном предложении должна не превышать 50,7 %. Например, ответственность именно за половину объема контракта уже устроит ЛПР(1) по уровню принимаемого риска.

Таблица 5

Распределение вероятностей потерь для ЛПР(1) при доле 50% участия в предложении

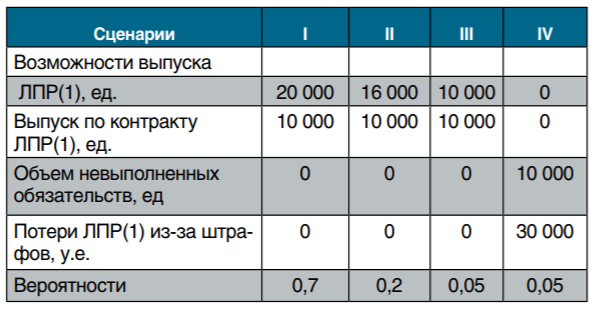
Удостоверимся, что участие в исходном предложении с долей 50% будет для ЛПР(1) приемлемым. Распределение возможных потерь из-за рассматриваемых рисков для такой ситуации представим в табл. 5. Соответствующие средние ожидаемые потери (как показатель чистого риска) составят 1 500 у.е. Такой показатель риска устроит ЛПР(1). Более того, снова убеждаемся в следующем: найденная оценка для доли участия (50%) для ЛПР(1) в анализируемом предложении и в формате концепции чистых рисков тоже оказалась заниженной. Причина этого — та же, что указывалась выше.

При желании менеджер может провести более детальные/точные расчеты для оценки приемлемой доли участия ЛПР(1) в предложении бизнеса. Например, проверим, будет ли приемлемой для ЛПР(1) участие в реализации контракта на 80%. Соответствующие средние ожидаемые потери со- ставят 3 300 у.е. при доле 80%. Как видим, чистый риск, который соответствует ситуации при α =0,8 (когда ЛПР берет на себя исполнение 80% объема контракта) также вполне приемлем для ЛПР(1) в формате рассматриваемой здесь концепции чистых рисков. Поэтому, если есть возможность выбора, то можно выбрать любое значение параметра α из области 0,5 ≤ α ≤ 0,8.

Далее обратим внимание на следующее. Если ситуация в бизнесе позволит ЛПР(1) принять лишь частичное участие в исполнении контракта (например, как отмечалось выше на 80%), то чтобы обеспечить производство недостающих 4 000 единиц продукции для соответствующего заказа потребуется привлечение дополнительных партнеров. В таких случаях задача перераспределения рисков может оказаться дополненной задачей выбора соисполнителя/ партнера.

Пусть в условиях анализируемой ситуации требуется привлечь партнера для производства 4 000 единиц продукции. Пусть имеется три альтернативы — поставщики ЛПР(2), ЛПР(3) и ЛПР(4). Распределение производственных мощностей этих возможных/доступных для выбора партнеров представлено в табл. 6. Требуется выбрать наилучшую альтернативу (партнера), минимизирующую риск в формате концепции чистых рисков.

Таблица 6

Распределение производственных мощностей у ЛПР(2) — ЛПР(3)

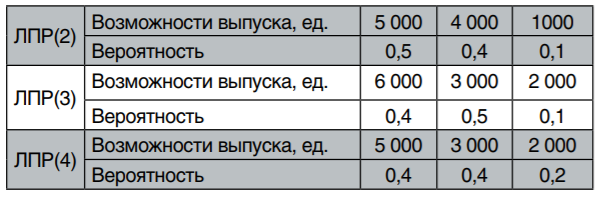
Поскольку в формате этой задачи управления риском нас интересуют именно потери (формат концепции чистых рисков), то представим соответствующее распределение вероятностей случайных величин потерь в табл. 7.

Таблица 7

Распределение вероятностей потерь у ЛПР(2) — ЛПР(3)

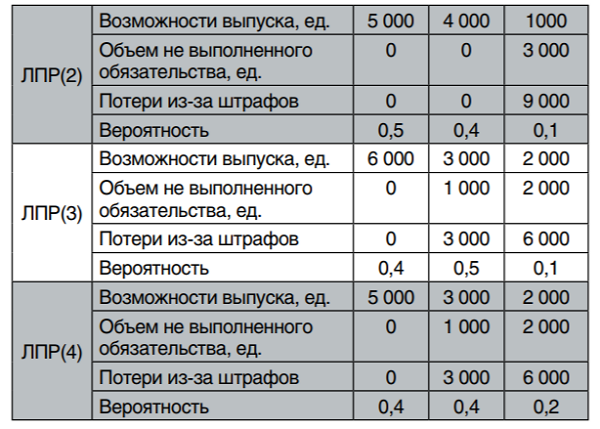
Рассчитаем соответствующие средние ожидаемые потери (как показатель риска в формате концепции чистых рисков). Обозначим такие потери в случае выбора в качестве партнера ЛПР(i) через П(i). Тогда имеем:

П(₂) = 0*0,5+ 0*0,4+9000*0,1 = 900 у.е.;
П(₃) = 0*0,4+ 3000*0,5+6000*0,1 = 2 100 у.е.;
П(₄) = 0*0,4+ 3000*0,4+6000*0,2 = 2 400 у.е.;

В соответствии с требованием рассматриваемой ситуации, как наилучшая альтернатива, минимизирующая чистый риск, будет выбор ЛПР(2) в качестве партнера для реализации 20% заказа. Обратим внимание на следующее. Задача выбора наилучшей альтернативы могла быть сформулирована и в формате концепции теории надежности. В этом случае оптимизировался бы следующий параметр: требовалось бы найти альтернативу, для которой вероятность срыва порученного объема (4 000 ед.) заказа была бы наименьшей. Обозначим вероятность срыва выпуска указанной доли заказа для ЛПР(i) через P(i). Тогда, в соответствии с данными табл. 7 имеем:

P(2) = 0,1 P(3) = 0,5+0,1 = 0,6;
P(4) = 0,4+ 0,2 = 0,6.

Как видим, в этой ситуации наилучшей альтернативой, минимизирующей вероятность срыва выпуска доли госзаказа, также будет выбор ЛПР(2).

Замечание. Расчеты в условиях рассматриваемой ситуации были проведены в предположении независимой реализации каждым из партнеров своей доли заказа. Подчеркнем, что поставленная задача перераспределения риска может быть решена и на основе концепции риска [1, 6], учитывающей отношение ЛПР к риску. В таком случае необходимо определить такое значение параметра α, при котором баланс между риском и доходом будет наиболее предпочтительным для ЛПР с учетом его индивидуального отношения к риску. С более широким спектром вопросов о возможностях перераспределения риска можно ознакомиться в книге «Управление рисками в логистике» [6].

Результаты были получены при участии проф. Бородецкого Г.Л.

Библиографический список

1. Бродецкий Г.Л. Моделирование логистических систем. Оптимальные решения в условиях риска. — М.: Вершина, 2006.

2. Иванов Д.А. Управление цепями поставок / Д.А. Иванов — СПб.: Изд-во Политехн. ун-та, 2009.

3. Корпоративная логистика. / Под ред. проф. В. Сергеева — М.: «Инфра-М», 2006

4. Логистика: Учебник / В.В. Дыбская, Е.И. Зайцев, В.И. Сергеев, А.Н. Стерлигова; под ред. В.И. Сергеева — М.: Эксмо, 2008.

5. Сток Дж. Р., Ламберт Д.М. Стратегическое управление логистикой: Пер. с англ. изд. — М.: ИНФРА-М, 2005.

6. Управление рисками в логистике: учеб. пособие для студ. учреждений высш. проф. образования / Г.Л. Бродецкий, Д.А. Гусев, Е.А. Елин — М.: Издательский центр «Академия», 2010.